Imagen del SARS-CoV-2, agente que produce la enfermedad COVID-19 (obtenida en el Instituto de Biología Celular y Neurociencias “Profesor E de Robertis”, CONICET-Facultad de Medicina (UBA), junto con científicos del Servicio de Virosis Respiratorias del Departamento de Virología del Instituto Nacional de Enfermedades Infecciosas (INEI) ANLIS-Malbrán y del Servicio de Microscopía Electrónica).

Publicado: 17 de abril de 2020.

Última actualización de datos: 09 de junio de 2020.

Desgraciadamente, el crecimiento de contagio de la enfermedad COVID-19 causada por el virus SARS-CoV-2, se comporta de una manera que puede ser modelada muy bien con funciones exponenciales. Por ello, se habla de que el crecimiento de contagios es exponencial.

En este artículo se dan lineamientos generales sobre ciertas características de estas funciones, que permiten visualizar y comprender a qué se refieren los científicos con aplanar la curva y concretamente a qué curva se refieren. También en forma sencilla con números y gráficos, se explican los efectos positivos alcanzados con la implementación del aislamiento social total, preventivo y obligatorio.

(Se recomienda para una cómoda lectura, acceder al sitio desde una PC y no desde un celular)

COVID-19: La pavorosa potencia de una función exponencial

Dr. Luis Mammana

Vicedirector del Complejo Astronómico El Leoncito (CASLEO-CONICET /Universidad Nacional de La Plata/ U. N. Córdoba/ U. N. San Juan)

Astrónomo Residente

Una adivinanza

Le propongo la siguiente adivinanza: si doblamos una hoja de papel 50 veces sobre sí misma, ¿la altura a la que llegaremos será similar a...?

1) el espesor de un teléfono celular (6 mm) o menos,

2) el alto de una tapita de agua mineral (1 cm),

3) el alto de un naipe (9 cm),

4) el alto de una latita de cerveza (16 cm),

5) la altura de una mesa (80 cm),

6) el alto de una puerta (2 m),

7) la altura del Obelisco de la ciudad de Buenos Aires (68 m),

8) la altura de la Torre Eiffel (300 m),

9) la distancia media entre la Tierra y la Luna (385 000 km),

10) la distancia media entre Venus y el Sol (107 millones de km),

11) la distancia media entre la Tierra y el Sol (150 millones de km).

La respuesta correcta es la opción 10). Sí, créame, si doblamos una hoja de papel 50 veces llegaremos a un pavoroso espesor similar a la distancia media que hay entre el planeta Venus y el Sol: la friolera de 107 millones de km. Es más... en realidad el espesor conseguido será algunos millones de kilómetros más.

Ahora que logré captar su atención, y antes de demostrarle con cuentas precisas mi afirmación (en Matemáticas hay que demostrarlo todo, inclusive que 1 es mayor que 0 -sí, eso también hay que demostrarlo-), hablemos de la espeluznante potencia de crecimiento que tiene una función exponencial.

Sin aburrirlo con tecnicismos, diré que se trata básicamente de una función con una base (un número dado constante) y un exponente que varía (la variable de la función).

Si la base es, por ejemplo, el número 2, entonces f(t) = 2^t es una posible función exponencial de base 2 y exponente variable t. Así, si la variable t toma el valor t = 1, entonces la función adopta para ese valor el número f(1) = 2¹ = 2. Si t = 2 la función valdrá f(2) = 2² = 4. Con t = 3, f(3) = 2³ = 8. La ferocidad de crecimiento de esta función es tal que con sólo doblar la cifra apenas 20 veces (t = 20), la función llega nada menos que a f(20) = 2²⁰ = 1048576, o sea, ¡más de 1 millón! Y claro, duplicando 21 veces, se superarán los 2 millones, porque sencillamente cada valor que fabrica esta función (2, 4, 8, 16, 32, 64, ...), siempre duplica al anterior.

Así como esa función exponencial tiene como base al número entero 2, una muy usada en Matemáticas es aquella que tiene como base al número irracional e ≈ 2.72. Por ello, otra función exponencial posible (dentro de las llamadas funciones exponenciales naturales) será g(t) = e^t, y es una variante de esta función la que emplearé más adelante.

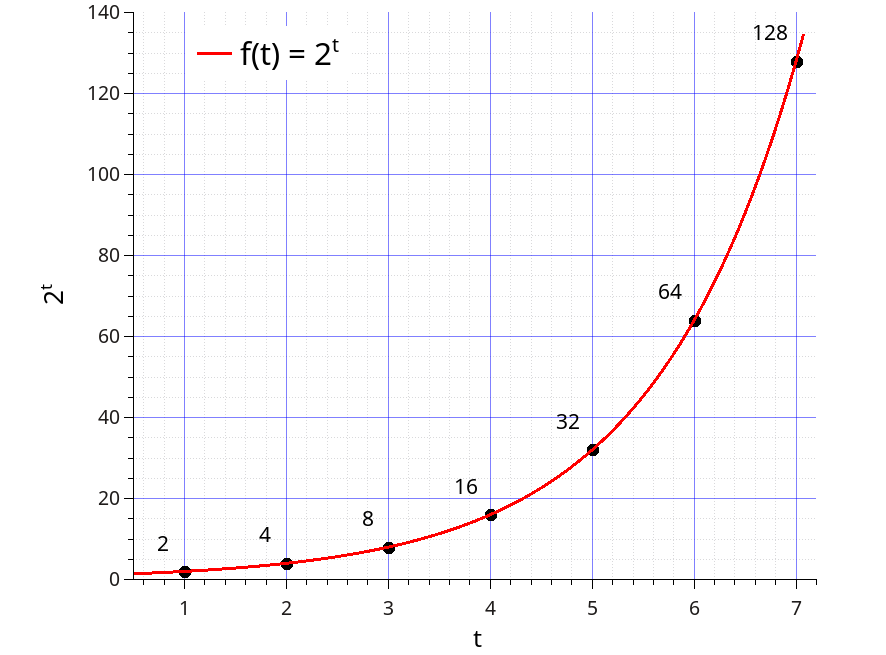
Para ilustrar lo dicho hasta ahora, hagamos un gráfico de la función exponencial f(t) = 2^t, con el fin de darnos una idea del monstruoso crecimiento que tiene la misma a medida que aumentamos la variable (t = 1, 2, 3, 4, 5, 6, ...):

Fig. 1. Gráfica de la función exponencial f(t)=2^t.

Si la curva sube a ese ritmo, imaginemos con esa misma escala cuán largo tendrá que ser el cuaderno donde la dibujamos como para que nos entre el gráfico cuando lleguemos nomás hasta t = 20.

Volvamos ahora sí a la pregunta que nos formulamos, y demostremos la respuesta:

Dado que una hoja de papel común tiene un espesor aproximado de una décima de milímetro, esto es 0.1 mm, si la doblamos 1 vez, tendremos un espesor igual a 2 veces 0.1 mm, o sea 2 x 0.1 mm. Como 2 = 2¹, podemos escribir 2 x 0.1 mm = 2¹ x 0.1 mm (el 1 del exponente nos dice que hemos doblamos la hoja una vez). Si la volvemos a doblar, tendremos un espesor el doble del anterior: 2 x (2 x 0.1 mm) = 4 x 0.1 mm. Como 4 = 2², podemos escribir 2² x 0.1mm (y nuevamente, en este caso el exponente 2 nos dice que hemos doblado la hoja 2 veces). Si la doblamos por tercera vez sobre sí misma, estaremos duplicando el valor anterior: 2 x (4 x 0.1 mm). Esto es 8 x 0.1 mm. Como 8=2³, tendremos: 2³ x 0.1 mm (nuevamente, el exponente 3 nos dice que doblamos nuestra hoja una tercera vez). Así siguiendo, si doblamos la hoja 50 veces llegaremos a un espesor igual a 2⁵⁰ x 0.1 mm. Ahora, como una calculadora cualquiera nos dirá que 2⁵⁰ = 1.126 x 10¹⁵,  el espesor será igual a (1.126 x 10¹⁵) x 0.1 mm = 1.126 x 10¹⁴ mm.

* Resumiendo:

Doblamos 1 vez (2¹ = 2), obtenemos: 2 x 0,1 mm = 0.2 mm.

Doblamos 2 veces (2² = 4), obtenemos: 4 x 0,1 mm = 0.4 mm.

Doblamos 3 veces (2³ = 8), obtenemos: 8 x 0,1 mm = 0.8 mm.

.

.

.

Doblamos 50 veces (2⁵⁰ = 1.126 x 10¹⁵), obtenemos: 1.126 x 10¹⁵ x 0.1 mm = 1.126 x 10¹⁴ mm.

Finalmente, pasando de unidades de mm a km, el espesor al que se llega después de haber doblado la hoja 50 veces será igual a 1.126 x 10¹⁴ x 10^-6 km = 112600000 km, es decir, un espesor que supera en más de 5 millones de kilómetros la distancia media que separa al Sol del planeta Venus.

Como ya se habrá dado cuenta el lector, el responsable de este resultado poco intuitivo es, en este ejemplo en particular, la distracción o el desconocimiento de a cuánto asciende el astronómico número 2⁵⁰, un enorme número de 15 cifras. En el caso general, el desconocer o distraerse no tomando conciencia del aterrador crecimiento que tienen las funciones exponenciales, puede llevarnos a situaciones inmanejables.

Una nota curiosa es que el récord mundial sobre la cantidad de veces que uno puede doblar una hoja de papel está en unas 13 veces. Si uno lo intenta, difícilmente supere las 8 veces con mucho esfuerzo.

Para quien no quiera hacer tanta fuerza, le propongo ir cortando cada pliegue a medida que realiza una “doblada” y vaya apilando las mitades que vaya obteniendo.

¡Ah!...le aviso que si en lugar de doblar la hoja 50 veces decide doblarla 63 veces, el espesor será más grande que el diámetro del Universo conocido, esto es, 8.8 x 10¹⁷ km = 8800000000000000000 km. Le sugiero no intentarlo.

COVID-19

Desgraciadamente, el crecimiento de contagio de la enfermedad COVID-19 causada por el virus SARS-CoV-2, se comporta de una manera que puede ser modelada muy bien con funciones exponenciales. Por ello, se habla de que el crecimiento de contagios es exponencial. Y dado que, como vimos, estamos hablando de funciones que crecen de una manera pavorosa en poco tiempo, si estamos distraídos o desconocemos su poder -y ya no estamos hablando de estar doblando una simple hoja de papel-, el resultado puede ser tristemente catastrófico.

Un detalle que la convirtió en pandemia, es su bajo índice de letalidad. El Ébola, por ejemplo, con un índice de letalidad que llegó al 90% en ciertos brotes, no se convirtió en pandemia porque si bien era muy contagioso, los afectados no daban tiempo a expandir la enfermedad porque morían pronto.

Se han venido publicando en distintos medios muchos gráficos que ilustran cómo ha ido creciendo el número de casos de contagio comprobados, pero ninguno da las ecuaciones que utilizan para interpolar los datos. En este artículo mostraré gráficos y las ecuaciones que tuve que ajustar para realizar los mismos.

Si ud. no está familiarizado con expresiones matemáticas explícitas y no quiere tomarse el trabajo de ahondar en ellas, puede pasarlas por alto... no son fundamentales en la idea general que pretendo transmitirle.

Comenzaré explicando sencilla y brevemente los términos interpolar y extrapolar datos de una muestra, porque nos servirán para comprender dichos gráficos (Fig. 2).

(hacer clic en la figura para ampliar)

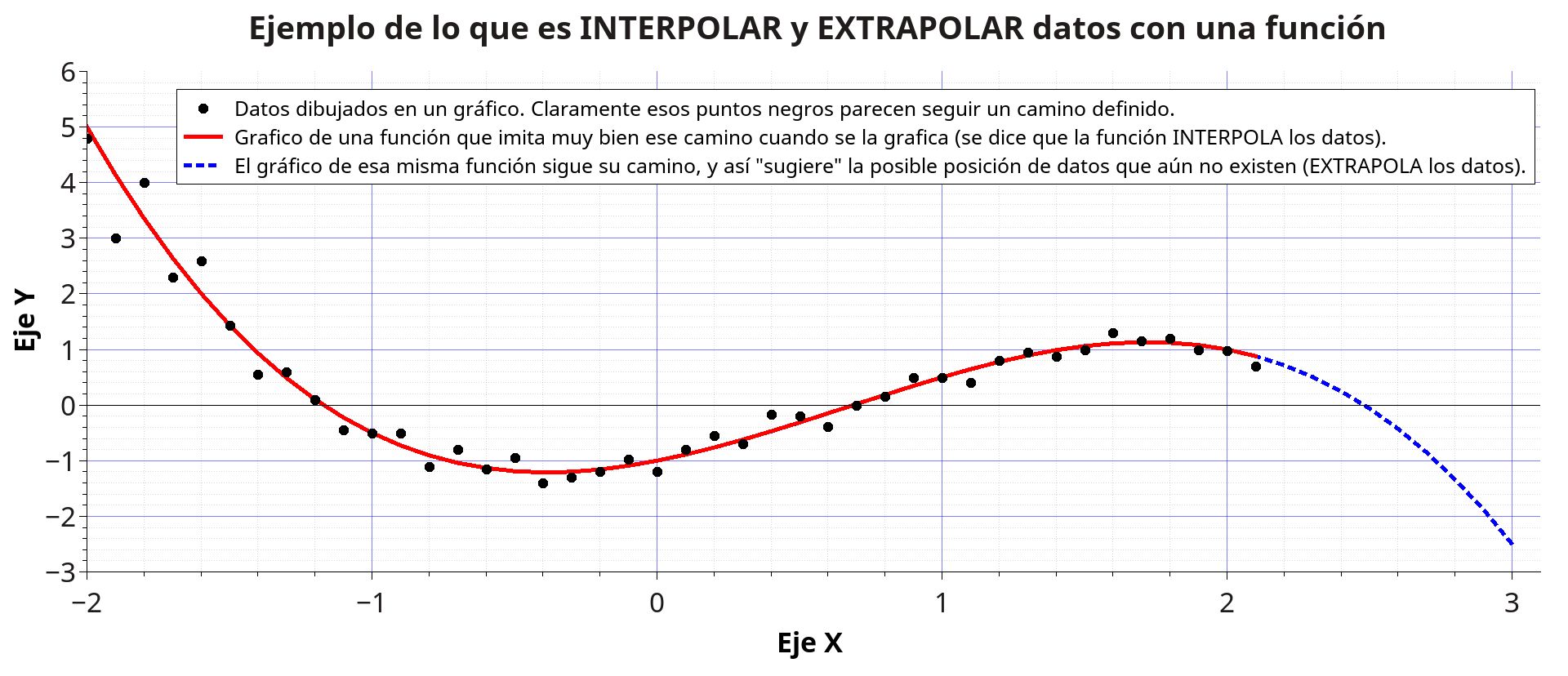Fig. 2. Una función interpolando y extrapolando datos.

Interpolar datos (puntos sueltos) dispersos en un gráfico, en pocas palabras, es trazar la curva entre ellos que mejor represente el camino que parecen seguir. Ello se consigue encontrando la función más adecuada, aquella que graficándola como hicimos con f(t) = 2^t, pase en una suerte de compromiso lo más cerca posible de todos los puntos del gráfico. Para interpolar, por ejemplo, una muestra con sólo 95 datos (que pueden ser los primeros 95 días de un experimento), naturalmente sólo podremos usar esos 95 datos porque no tenemos más, y por lo tanto, la curva que se traza entre ellos se corta en el último punto de la muestra.

Ahora bien, si la interpolación fue exitosa, esto es, si se logró obtener una función a partir de los datos tal que al graficarla su gráfico pase, como decía, en una suerte de compromiso lo más cerca posible de todos los puntos dispersos de la muestra, podremos utilizar la expresión de esa función para dibujar su curva más allá de los datos, allí donde ya los datos no llegan. A eso se le llama extrapolar una muestra de datos. La utilidad que tiene extrapolar es poder predecir con cierto margen de error qué pasará a futuro, por ejemplo para el día t = 100 del cual no teníamos datos. En definitiva, extrapolar usando una fórmula de interpolación es predecir con base científica cómo se comportará el estudio que se está modelando a futuro, o cómo se comportó en el pasado, extendiendo la curva hacia atrás. Es muy importante tener especial cuidado en el uso de las extrapolaciones porque siempre es muy arriesgado extrapolar yéndose muy hacia adelante o muy hacia atrás respecto de la muestra con la que se cuenta.

¿A qué se refieren con aplanar la curva de contagios, y a qué curva precisamente se están refiriendo?

Se habla mucho de que con la cuarentena se busca aplanar la curva de contagios con el fin de que el sistema de salud no colapse, y de esa manera, todos los infectados puedan ser atendidos en las mejores condiciones posibles. Pero ¿a qué se refieren concretamente con aplanar una curva y de qué curva hablan?

Tomando datos del Ministerio de Salud de la Nación (que incluyen los casos registrados en las Islas Malvinas, como era de esperarse), realicé una serie de interpolaciones de dichos datos, y luego de haber hallado las funciones exponenciales que mejor ajustaban esa muestra, extrapolé a futuro la función que ajustaba el comienzo de la muestra, a fin de ver cuán eficiente estaba resultando la cuarentena.

Los datos a los que me refiero consisten en la cantidad de infectados detectados acumulados para cada día desde el primer contagio detectado el 03 de marzo (al que llamaré día t = 1 de la muestra en los gráficos), hasta el día 05 de junio (día t = 95). Hago hincapié en detectados, porque la muestra no refleja la cantidad de infectados reales que existen en la población, sino solamente en aquellos casos testeados que dieron positivo. Graficando dichas cantidades en función de los días, se obtienen los puntos negros del gráfico de la Fig.3, que representé en escala logarítmica para hacer más visibles los detalles.

(hacer clic en la figura para ampliar)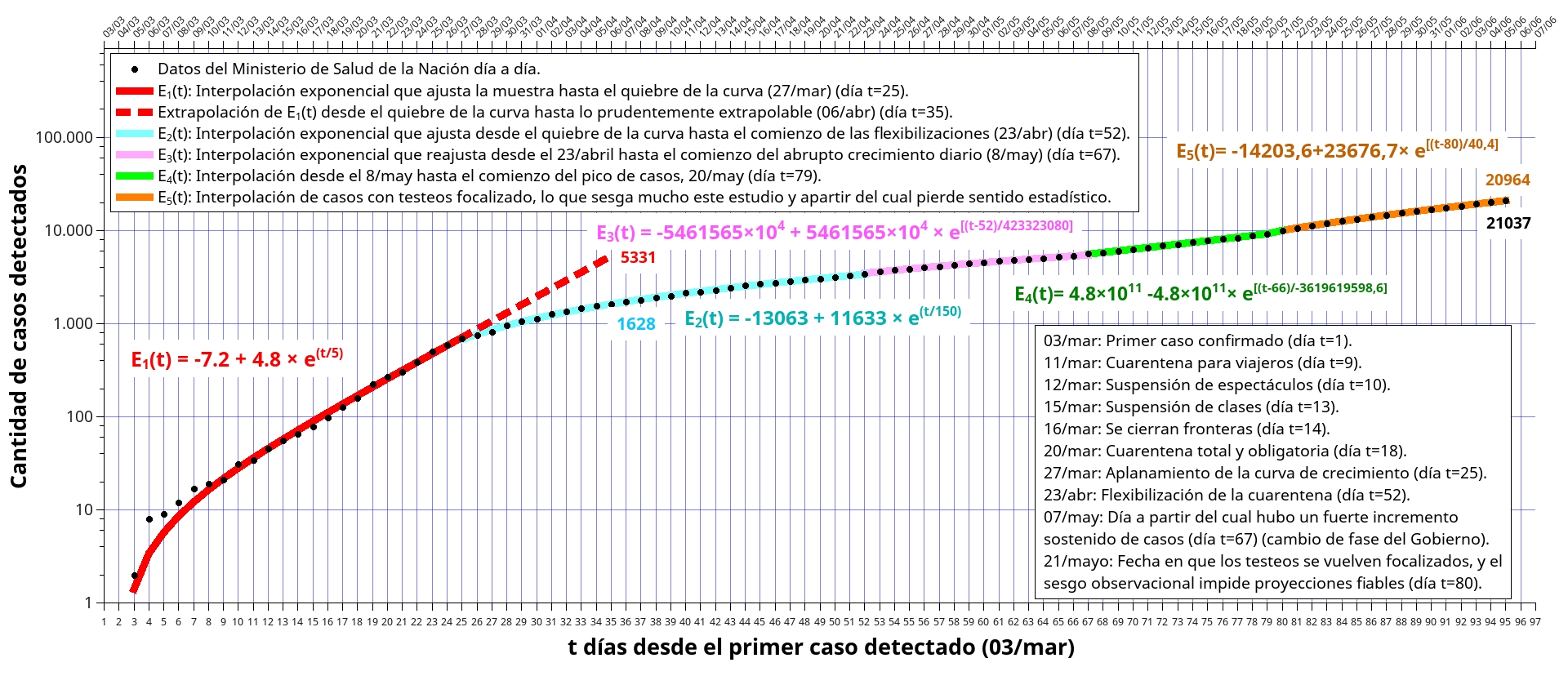Fig. 3. Gráfico de la cantidad acumulada de contagios detectados vs. días.

Lo primero que salta a la vista es que hay un quiebre en la muestra que se da entre los días 26 (t = 24) y 27 (t = 25) de marzo, haciendo evidente un aplanamiento de la curva de contagios producto, fundamentalmente, del aislamiento poblacional (cuarentena). La afirmación de que, efectivamente, el aplanamiento se da en esas fechas, será fundada al final de este artículo con argumentos matemáticos.

Interpolando los datos desde t = 1 hasta t = 25 se obtiene la función exponencial E₁(t), que si se la deja seguir (extrapolación) como si el quiebre (cuarentena) no existiera, la línea punteada llegaría a 5331 casos contagiados acumulados al 23 de abril (t = 35), fecha en la que se flexibilizó la cuarentena. Sin embargo, interpolando desde dicho quiebre con la función exponencial E₂(t), vemos que al 23 de abril llegamos a sólo 1622 casos (basta con reemplazar con una calculadora t=35 en mi fórmula de E₂(t), para llegar a ese resultado), muy en acuerdo con el dato dado por el Ministerio de Salud de la Nación para esa fecha, que fue de 1628 casos acumulados.

La conclusión más importante es que gracias a la cuarentena se logró detener el crecimiento un 70% en apenas 10 días, y sostenerse esa tendencia hasta a la baja hasta comenzado el pico. Cabe destacar que en virtud de lo expuesto sobre el enorme crecimiento de estas funciones en muy poco tiempo, un cambio importante en las condiciones de aislamiento, puede disparar la curva a límites indeseados.

Siempre teniendo la precaución de que este análisis no profundiza en cuestiones médicas, o del sistema de salud o sobre ciertas conductas poblacionales que pudieran introducir variables particulares, utilizando la expresión dada por la función exponencial E₃(t), uno podría estimar la cantidad aproximada de infectados que acumulará Argentina en una fecha futura dada, reemplazando en la variable t de la misma, la cantidad de días transcurridos desde el 03 de marzo (día t = 1) hasta la fecha elegida. Como aclaré antes, las extrapolaciones no deben ir muy lejos de la muestra porque las fórmulas dejan de tener validez. En este caso en particular, ello se debe a que, como la situación es muy dinámica, naturalmente las condiciones en las que construí las interpolaciones variarán en el tiempo por múltiples razones, y esas variaciones irán acumulando más y más errores cuanto más nos alejemos de esas condiciones iniciales, hasta que llegará un momento en el que las diferencias entre la realidad y lo que predicen mis ecuaciones serán inaceptables desde el punto de vista científico. Usualmente, uno no se excede yendo más allá en días, que los que posee la mitad de la muestra. Con una muestra de uns 65 días, no es recomendable usar, por ejemplo, la ecuación E3(t) más allá de unos 30 días después del 6 de mayo, esto es, no más allá de fines de mayo para ser conservadores.

Para terminar, algo había quedado por justificar: ¿Por qué estamos seguros que la curva se empezó a aplanar, digamos, desde el 27 de marzo? Que se vea a ojo en el gráfico no siempre es confiable y es, en todo caso, muy subjetivo. Pensemos en lo siguiente y demos así una explicación matemática. Un grupo de científicos del Instituto Balseiro, CONICET, CNEA y Universidad del Comahue (https://es-la.facebook.com/cyua.bariloche/) desarrollaron una idea para determinar el punto de inflexión de la curva. Yo le agrego a esa idea dos ajustes lineales que facilitan visualizar los resultados.

Supongamos que en algún hipotético país que no es la Argentina, en los días t = 1, 2, 3, 4, 5, 6 y 7 hubieran habido respectivamente 1, 6, 15, 30, 33, 33, 34 infectados acumulados. Lo que se ve es que, a partir del cuarto día, tendrán casi la misma cantidad de contagiados acumulados (un promedio de poco más de 32 por día). En otras palabras, la cantidad de contagios se frenó, lo cual se ve porque en esos últimos días la cantidad de infectados que suma un día es casi la misma que la que sumaba el día anterior.

Una forma matemática de interpretar ese hecho es teniendo en cuenta algo que todos sabemos y es que si dividimos entre sí dos números muy parecidos, la división nos dará casi 1. O sea que un criterio que puede utilizarse para medir cuándo los contagios empiezan a bajar, es ver desde cuándo la cantidad de contagiados acumulados hasta cierto día, dividida por la cantidad de contagiados acumulados al día anterior nos empieza a dar cerca de 1. De hecho, si los habitantes de ese país fueran muy afortunados y un día tienen la misma cantidad de contagiados acumulados que el día anterior (o sea, no tuvieron ningún infectado nuevo), esa cuenta les dará exactamente 1. Veamos esas divisiones en el caso de ese hipotético país:

6/1 = 6, 15/6 = 2.5, 30/15 = 2, 33/30 = 1.1, 33/33 = 1 y 34/33 = 1.03. Como vemos, la sucesión de cocientes será:

6, 2.5, 2, 1.1, 1, 1.03.

De dicha sucesión podemos inferir que dado que 33/30 = 1.1 es el primer número de la serie donde él y los restantes de la misma se aproximan mucho a 1, es entre los días t = 4 y t = 5 donde la cantidad de infectados nuevos se frena, lo que produce que en ese país la curva se quiebre y comience a aplanarse.

Con esta misma idea, y volviendo a los datos reales de nuestro Ministerio de Salud de la Nación, grafiqué los cocientes entre "días consecutivos vs. los días de la muestra" (Fig.4), y ajusté dos rectas (y₁(t) e y₂(t)) que interpolan las cruces, donde se ve claramente que a partir del 27 de marzo los cocientes (las cruces) se empiezan a acercar a 1 (ese 1 debe leerse en el eje vertical). De hecho, la sucesión de los cocientes a partir de ese día (t = 25 en la Fig.4), poseen una media (promedio de los valores) de 1.4 para los primeros días antes del quiebre, y de 1.1 -más cercano a 1- para el resto de la muestra.

La gran dispersión (“desparramo”, permítaseme el término) de los datos iniciales (ajustados por y₁(t)), se debe a las bruscas variaciones de cantidad de casos detectados acumulados en los primeros días con respecto al siguiente, y claramente, aunque el quiebre existe, esos primeros casos -que podrían excluirse del análisis-, lo exagera y lo deja más en evidencia.

(hacer clic en la figura para ampliar)

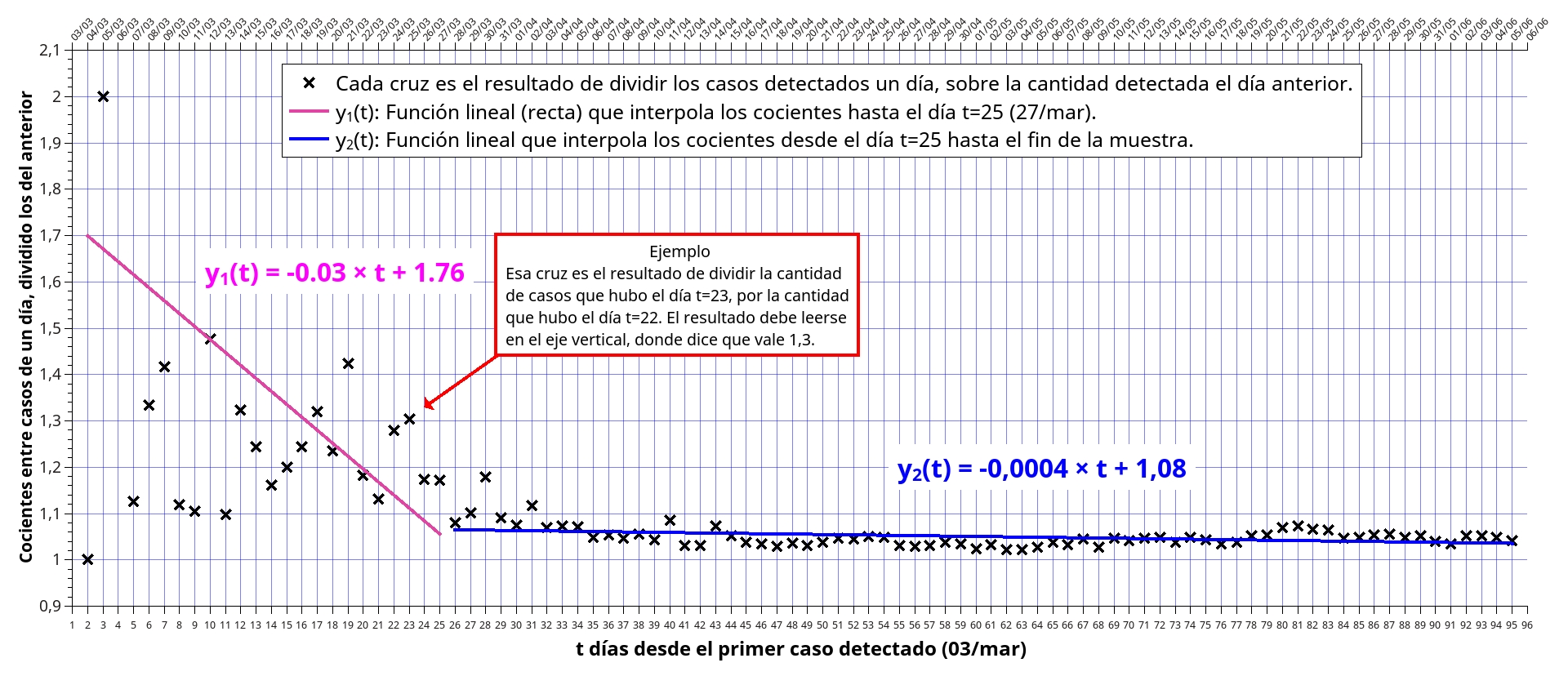Fig. 4. Ajustes mediante rectas de los cocientes entre las cantidades de infectados de días consecutivos.

Queda, entonces, así justificada la afirmación sobre que el aplanamiento de la curva de contagios se dio efectivamente entre el 26 y 27 de marzo, una semana después de impuesto el aislamiento social total, preventivo y obligatorio.